Princípios físicos envolvidos no funcionamento de um rotâmetro

Neste artigo iremos apresentar os principais princípios físicos que regem o funcionamento de um rotâmetro.

Sobre o rotâmetro

Um rotâmetro é um medidor de vazão de área utilizado para medir a vazão de líquidos e gases de diferentes opacidades e características físicas, em diversas aplicações.

Basicamente os rotâmetros consistem em um tubo de vidro borossilicato (ou plástico) e de um outro componente muito importante, conhecido como flutuador que, a depender do tipo de rotâmetro, poderá ser livre ou guiado.

Quando o fluido atravessa o tubo cônico, arrasta o flutuador para cima pela força da pressão diferencial.

Ao movimentar-se para cima, o flutuador aumenta a área de passagem do fluxo em relação ao tubo cônico e reduz a velocidade do fluido causando perda da pressão diferencial.

Quando é alcançado o equilíbrio entre sua massa e a pressão diferencial, o flutuador estaciona e proporciona a leitura da vazão.

Leis da física que regem o funcionamento de um rotâmetro

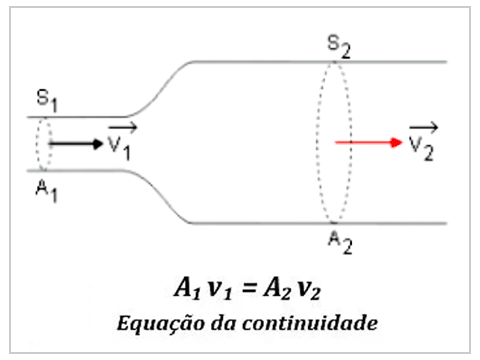
Equação da continuidade

A equação da continuidade, também chamada de lei da conservação da massa, nos mostra que em um escoamento em regime permanente, a massa do sistema é constante, em outras palavras, a vazão em massa que entra é igual a vazão em massa que sai.

Podemos então, escrever:

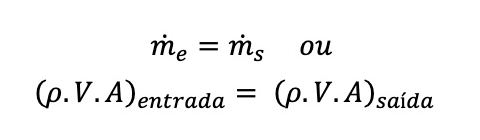
No caso de escoamentos incompressíveis ( p_e = p_s ) já considerando 1 como entrada e 2 como saída, como indicado na figura, temos:

 Assim, pela equação da continuidade podemos relacionar a variação de velocidades que acontece entre duas seções de área de seções diferentes.

Equação de Bernoulli

O princípio de Bernoulli, tem sua base na equação da continuidade, o conceito é o mesmo, porém desenvolvido para trabalharmos com pressões em líquidos, e nos dá uma equação que relaciona em um escoamento incompressível, as parcelas de energia cinética, gravitacional e de pressão.

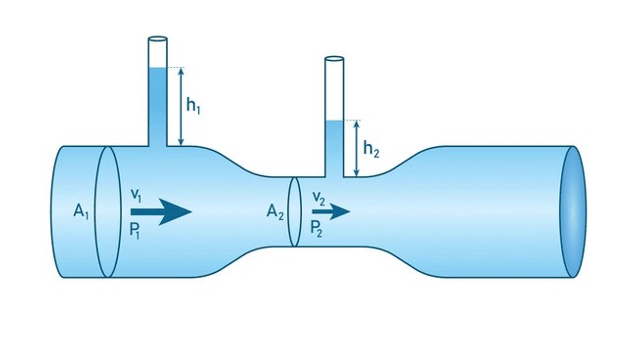
Escoamento incompressível

A equação é:

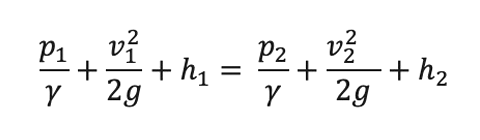
Onde:

Teorema de Torricelli

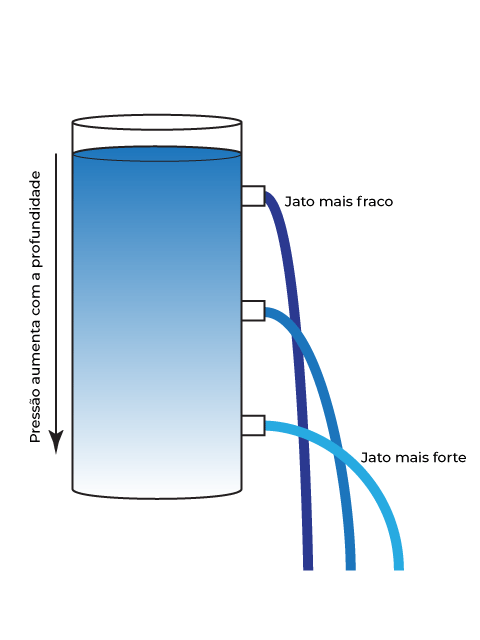
Esse teorema é um desenvolvimento da equação de Bernoulli, e nos dá a possibilidade de deduzir a velocidade de um fluido que passa por um orifício. Considerando um reservatório aberto para atmosfera e de grandes dimensões com altura de coluna de líquido e com um orifício em sua região inferior, teremos a dedução da equação de Bernoulli que nos dará o teorema de Torriceli:

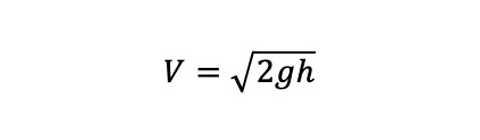
Onde:

Lei de Poiseuille

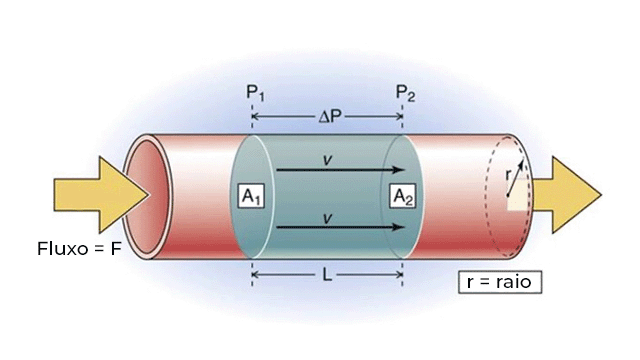
Essa lei nos permite relacionar vazão com a viscosidade, em um escoamento incompreensível de viscosidade baixa e que aconteça em um tubo de seção circular. Ela diz que:

Onde:

Similaridade entre gases ideais e vapores superaquecidos

Gases ideais são gases que suas partículas possuem colisões elásticas entre si, ou seja, conservam suas energia e momento linear pós colisão. Além disso, as partículas possuem velocidade média iguais, além de suas forças viscosas serem desconsideradas.

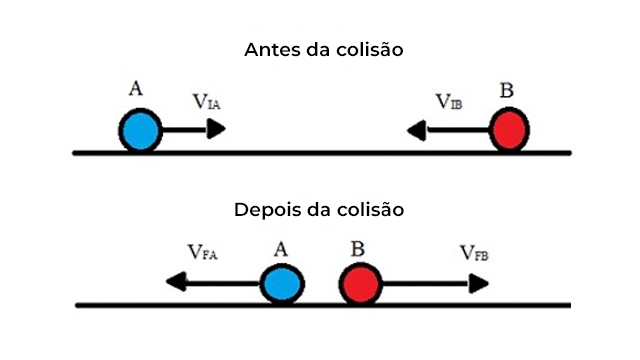
Colisão elástica dos gases ideais

Vapores superaquecidos tendem a se comportar de forma muito similar aos gases ideias, isso porque, seu nível de energia, faz com que as partículas entrem em movimentos desordenados e se afastem uma das outras, neutralizando, assim como os gases ideais, a viscosidade.

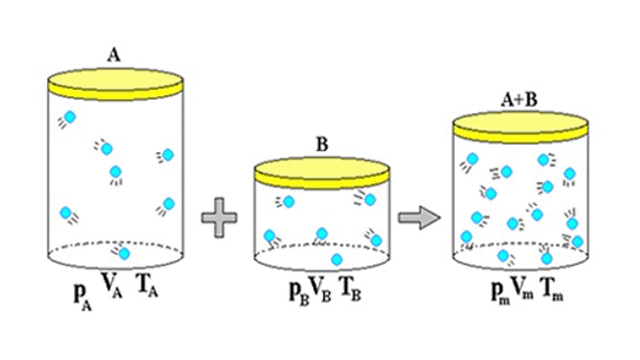
Estimasse que, o desvio entre o comportamento dos gases ideais e vapores superaquecidos são na ordem de 5%, diferença essa considerada baixa, dando segurança para realizar as aproximações.

Vale ressaltar também que, os gases ideias, seguem a equação de Clapeyron, equação essa que relaciona a temperatura, pressão, volume e o número de partículas de um gás ideal.

Essas similares, nos resulta na possibilidade de medir mais de um gás com o mesmo rotâmetro, portanto que saibamos a temperatura, densidade, pressão dos gases relacionados

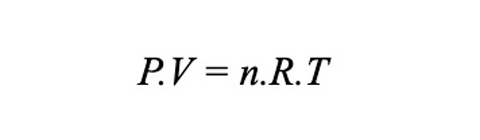
Onde:

Estimando o fluxo volumétrico em rotâmetros

Uma das maneiras de estimar o fluxo nos rotâmetros pode ser expressa pela forma abaixo:

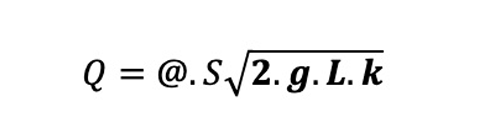
Onde:

A influência do número de Reynolds no rotâmetros

O número de Reynolds mede a relação entre as forças inerciais e as forças viscosas em um escoamento. Se ocorrer somente uma mínima variação no número de Reynolds devido a variações nas propriedades do líquido, as fórmulas são validas.

Portanto, no caso de rotâmetros, eles serão bastante fidedignos para números de Reynolds maiores do que 1000, onde a viscosidade apresenta valores muito baixos, pois o princípio do rotâmetro baseia-se na Equação de Bernoulli, onde o fluido não possui viscosidade.

Isto não quer dizer que não seja possível medir vazões de fluidos que apresentem viscosidades moderadas, como o óleo mineral, por exemplo. Basta para isto, inserir na fórmula da vazão fatores de correção.